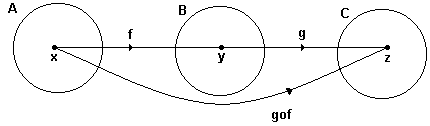
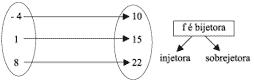
FUNÇÃO INVERSA
Dada uma função f : A e B , se f é bijetora , então define-se a função inversa f -1 como sendo a função de B em A , tal que f -1 (y) = x .
Veja a representação a seguir:
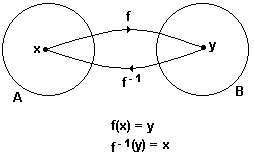
É óbvio então que:
a) para obter a função inversa , basta permutar as variáveis x e y .
b) o domínio de f -1 é igual ao conjunto imagem de f .
c) o conjunto imagem de f -1 é igual ao domínio de f .
d) os gráficos de f e de f -1 são curvas simétricas em relação à reta y = x ou seja , à bissetriz do primeiro quadrante .
a) para obter a função inversa , basta permutar as variáveis x e y .
b) o domínio de f -1 é igual ao conjunto imagem de f .
c) o conjunto imagem de f -1 é igual ao domínio de f .
d) os gráficos de f e de f -1 são curvas simétricas em relação à reta y = x ou seja , à bissetriz do primeiro quadrante .
Exemplo:
Determine a INVERSA da função definida por y = 2x + 3.
Permutando as variáveis x e y, fica: x = 2y + 3
Explicitando y em função de x, vem:
2y = x - 3 \ y = (x - 3) / 2, que define a função inversa da função dada.
Determine a INVERSA da função definida por y = 2x + 3.
Permutando as variáveis x e y, fica: x = 2y + 3
Explicitando y em função de x, vem:
2y = x - 3 \ y = (x - 3) / 2, que define a função inversa da função dada.
O gráfico abaixo, representa uma função e a sua inversa.
Observe que as curvas representativas de f e de f-1, são simétricas em relação à reta
y = x, bissetriz do primeiro e terceiro quadrantes.
y = x, bissetriz do primeiro e terceiro quadrantes.
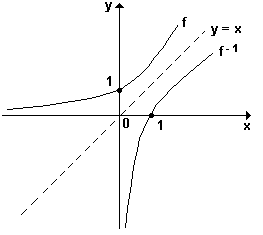
Exercício resolvido:
A função f: R ® R , definida por f(x) = x2 :
a) é inversível e sua inversa é f -1 (x) = Ö x
b) é inversível e sua inversa é f -1(x) = - Ö x
c) não é inversível
d) é injetora
e) é bijetora
A função f: R ® R , definida por f(x) = x2 :
a) é inversível e sua inversa é f -1 (x) = Ö x
b) é inversível e sua inversa é f -1(x) = - Ö x
c) não é inversível
d) é injetora
e) é bijetora
SOLUÇÃO:
Já sabemos que somente as funções bijetoras são inversíveis, ou seja, admitem função inversa. Ora, a função f(x) = x2, definida em R - conjunto dos números reais - não é injetora, pois elementos distintos possuem a mesma imagem. Por exemplo,
f(3) = f(-3) = 9. Somente por este motivo, a função não é bijetora e, em conseqüência, não é inversível.
Já sabemos que somente as funções bijetoras são inversíveis, ou seja, admitem função inversa. Ora, a função f(x) = x2, definida em R - conjunto dos números reais - não é injetora, pois elementos distintos possuem a mesma imagem. Por exemplo,
f(3) = f(-3) = 9. Somente por este motivo, a função não é bijetora e, em conseqüência, não é inversível.
Observe também que a função dada não é sobrejetora, pois o conjunto imagem da função f(x) = x2 é o conjunto R + dos números reais não negativos, o qual não coincide com o contradomínio dado que é
igual a R. A alternativa correta é a letra C.
igual a R. A alternativa correta é a letra C.
-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x
Observe, no diagrama de setas abaixo, a função f : A →B | f(x) = x – 5, que transforma os elementos de A nos de B:
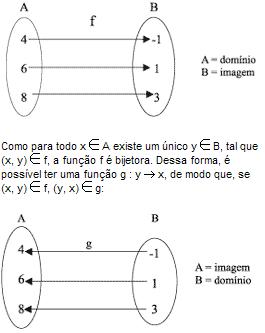
Conclusão: A condição necessária e suficiente para que uma função tenha inversa é que seja sobrejetora e injetora, ou seja, bijetora. No caso, temos que g é a função inversa de f.
Mais uma Videoaula para vocês !